Historia del cero

Podría decirse que surgió de forma independiente en dos lugares tan alejados como Mesopotamia y Mesoamérica. Dos civilizaciones que necesitaron crear el cero para necesidades diferentes.

Numeración maya Fuente: wikipedia commons
Licencia: GNU 1.2

En un lugar los antiguos babilonios necesitaban el cero para llevar la contabilidad. La escribían en tablillas de cerámica sin cocer mediante símbolos cuneiformes. Disponían de dos sistemas de numeración, uno decimal y otro sexagesimal que empleaban de forma combinada. Esto es, de 1 a 60 sistema decimal y de 60 en adelante sexagesimal.
Es en éste último donde usaban un símbolo para denotar la posición. Un sistema posicional permite que con muy pocos signos se pueda representar prácticamente cualquier cifra. Un ejemplo, para diferenciar 18 de 108. Ese símbolo intermedio, entre el 1 y el 8, el cero, era el que ellos representaban mediante dos espigas inclinadas. Esto fue hacia el año 300-400 a.c.

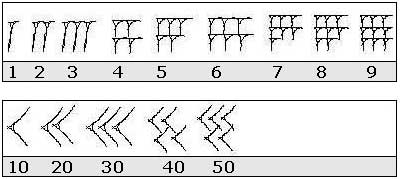
Numeración babilonia

Por otro lado tenemos a los mayas, situados en la zona Sur de México, Guatemala, y el norte de Belize. Esta civilización alcanzó su esplendor en el primer milenio de nuestra era. En torno al año 665 ya tenían un sistema numérico de valor por posición vigesimal (base 20) con un símbolo para el cero. Es importante destacar que el cero ya se usaba antes de esa fecha, y que tenía más aplicaciones que la posicional.
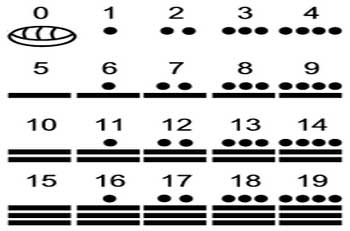
Es imposible resumir en esta entrada la complejidad e interés de las matemáticas desarrolladas por los mayas. Al parecer las motivaciones fueron astronómicas y religiosas. Los mayas tenían varios calendarios diferentes, cuatro, con diferentes duraciones. Es probable que la invención del cero pudiese deberse a los olmecas, una civilización anterior a los mayas ubicada en los actuales estados de Tabasco y Veracruz. Desgraciadamente su descubrimiento no paso a otras culturas más allá de los mayas.
Volviendo a Babilonia, su sistema numeral parece que fue conocido por los griegos a raíz de la conquista de Mesopotamia por Alejandro Magno (331 a.c.). Fue así como pasó a Grecia y llegó a la India (aprox. año 650 d.c.). No obstante el cero permaneció y alcanzó un importante desarrollo en la India a la par que fue olvidado en Occidente. El primero registro datado con exactitud del uso indio del cero y sobre el que todos están de acuerdo fue escrito en el año 876 d.c.
Es cuando entran en escena los árabes que al contactar con los indios (s IX-X aprox) conocen el cero y lo traen de nuevo a Europa. No sólo trajeron el cero, sino las cifras para representar los numerales en un sistema decimal (base 10). De ahí el nombre de cifras arábigas. A China llegó en los s. XIII-XIV donde fue desarrollado.
Los comerciantes italianos, fueron sus impulsores. Y uno de los matemáticos italianos más conocidos, Fibonacci (1202), basándose en la obra del sabio arabe Al Khwarizmi (año 825) lo difundió por Europa. No obstante el cero no gozó de la misma importancia que el resto de numerales. Así tenemos la paradoja de que Cardan resolvió ecuaciones de tercer y cuarto grado sin usar el cero.
Ya en el siglo XVII el cero consiguió la importancia que sin duda se merecía. Y hasta nuestros días, en que el cero es la base de las matemáticas, las finanzas, los complejos cálculos científicos, etc. Curiosamente la base de la informática, la lógica binaria está basada en unos y... ¡ceros!. ;)
Enlaces relacionados:
» La historia del cero. por JJ O'Connor/EF Robertson. [english] [Traducción] . :)
» Historia del cero, wikipedia english.
» Numeración babilonia. por JJ O'Connor/EF Robertson. [english] [Traducción]
» Matemática babilonia wikipedia. [english]
» Contando en Babilonia por Michael Fowler. Traducción de Lydia Alvarez.
» Numeración maya wikipedia.
» Numeración maya por JJ O'Connor/EF Robertson. [english]
» El cero y la nada por Pablo Capanna.